Moral Decision-Making by Analogy: Generalizations vs. Exemplars

Supplementary Materials

Joseph A. Blass, Kenneth D. Forbus Qualitative Reasoning Group, Northwestern University 2133 Sheridan Road, Evanston, IL 60208 USA Contact: joeblass@u.northwestern.edu

Having our machines learn our own moral norms: in the paper we state that “[society’s] systems need to learn and reason the same way we do in moral domains if we are ever to trust them to make the right decision in high-stakes environments, such as driving a car on the highway”. An exception clearly needs to be made for criminals and psychopaths, who should not be able to program their machines to advance their own agendas at the expense of others. But the importance of having machines make decisions in line with their owners’ norms becomes clear if you consider a situation where a self-driving car is heading towards a one-lane bridge. Imagine that there is an automated system in the bridge that communicates with the car and tells it that there is no one else on the bridge, and no cars approaching the bridge, so the car is moving quickly. Finally, imagine that right before the car reaches the bridge, a small child bursts forth from a bush right in front of the bridge, chasing a ball. The car does not have time to stop, and has to choose between swerving off the road and going off a cliff, killing its passenger, versus hitting the child.

Two perfectly sane, healthy, moral people might want to do very different things in this situation, and their cars should as well. The car does not have the right to kill its passenger if the passenger thinks that ultimately the child is responsible for his actions and that the passenger does not deserve to die over the child’s carelessness. Similarly, the car does not have the right to force its passenger to be partially complicit in the death of a child if the passenger would have driven the car off the cliff had they been driving. Most importantly, the decision should ultimately rest with the passengers of the car, not the software engineers who created its programming.

Practically speaking, whoever builds a self-driving car would probably deal with this situation and everything like it by having the car slam on the brakes and hope for the best, since that will provide the least legal liability, but the thought experiment is nonetheless constructive.

Additional facts added to solved scenarios: when a human child is told a moral parable by their parent, they are not only told what the right thing to do is, but why. We wished to simulate this as well as provide MoralDM’s analogical reasoning system with appropriate higher-level, structural facts to reason with. To that end, we appended not only the appropriate decision fact to the solved scenarios, but a justification fact as well. For example, for the scenario where a person has the choice between letting a bomb in a restaurant explode and kill nine people or toss it outside where it will kill one person, the added facts (presented with their translation into plain English) were:

(implies Because:

(and

(protectedValueChoice throw18421) throwing the bomb violates a Protected Value; (protectedValueChoice Inaction18657) doing nothing violates a Protected Value; (uninferredSentence it is not the case that throwing the bomb affects

(affectsSigLargerGroup throw18421) significantly more people than the alternatives;

(uninferredSentence it is not the case that doing nothing affects

(affectsSigLargerGroup Inaction18657)) significantly more people than the alternatives; (directlyResponsible you18016 throw18421) you18016 is directly responsible for throwing it; (uninferredSentence but it is not the case that the actor you18016 is

(directlyResponsible you18016 Inaction18657)) directly responsible for doing nothing;

(preventsAlternativeNegativeOutcome that throwing the bomb prevents

throw18421) a negative outcome;

(uninferredSentence but that the harm caused by throwing the

(usedAsMeansToPreventNegOutcome bomb is not used as the means to prevent

throw18421)) the negative outcome;

(rightChoice throw18421)) therefore throwing the bomb is the right thing to do.

(makeDecision you18016 throw18421) The actor you18016 decided to throw the bomb.

• (uninferredSentence <fact>) indicates that <fact> cannot be reasoned to, and that due to the closed-world assumption is taken to be false. You can read (uninferredSentence

  <fact>) as “it is not the case that <fact>”.

• The predicate (usedAsMeansToPreventNegOutcome <action>) means “the negative outcome of [action] is directly used to prevent another negative outcome from occurring”, which is not clear from the name of the predicate alone. The shorter name is used for length considerations. This fact is used to distinguish between cases where the negative outcome of an action directly prevents another negative outcome (throwing a person on a bomb saves nine other people, and that person’s death is causally necessary to saving the nine) from those where it does not (throwing the bomb outside, as above, kills an innocent bystander, but that death is not causally necessary to saving the nine, but is rather an unfortunate side effect).

• Each event and actor token has a string of numbers appended to it to make clear that these refer to particular events and actors in this particular context, and that throw18421 exclusively refers to throwing this particular bomb on this particular patio, and not to any throwing event. These are discourse variables automatically produced by the natural language understanding system.

Accuracy by composition of training set: The following charts are provided to further contextualize our results.

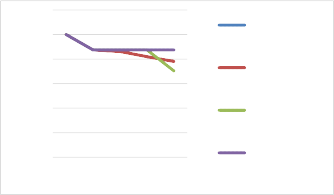
Accuracy by matches in training dataset: Accuracy by confounds in training dataset:

1.2

Proportion Accurate

1

0.8

0.6

0.4

0.2

0

0 1 2 3

Generalizations Only

Generalizations and Cases

Cases Only BestSME

1.2

Proportion Accurate

1

0.8

0.6

0.4

0.2

0

0 1 2 3 4

Generalizations Only

Generalizations and Cases

Cases Only

BestSME

Number of Matches in Training

Number of Confounds in Training

If there was even a single matching case in the training set, all techniques were likely to find the correct answer (unsurprisingly, if there were no matches, no techniques could infer the correct answer). Not all techniques were perfect, but all were close to 100%. However, as the number of confounds in the training set increased, BestSME and MAC/FAC using Generalizations only plateaued and continued to perform well, whereas accuracy MAC/FAC using Cases only and using Generalizations and Cases continued to degrade.

Statistical Analyses: We performed a logistic regression to determine the influence of experimental technique, training case library size, and condition given case library size. We found a significant interaction of condition and case library size, as well as a main effect of case library size, but only a marginal main effect of technique. To determine the relative rates of improvement of each condition, as indicated by the logistic regression, we calculated Pearson’s correlations, and used Fisher r-to-z transformations to compare correlations. MAC/FAC over generalizations alone and Best SME performed identically, so their correlation coefficients were the same and did not differ. MAC/FAC over generalizations and cases and over cases alone did not differ significantly. Given our findings from the logistic regression over our entire dataset and our hypotheses, we decided to perform additional logistical regressions over only those trials using small training case libraries, and over those trials using only large training case libraries. As predicted, we found that condition did not affect performance for small case libraries but had a significant impact on performance with larger case libraries. To investigate relative performance of experimental techniques with large case libraries we performed t-tests; to reduce the chance of Type I error while keeping our cutoff for statistical significance reasonable, we sought to minimize the number of tests performed, comparing each technique’s performance across all trials with large case library sizes, rather than at each individual training case library size. With only three comparisons, we used Bonferroni’s correction to calculate the level of statistical significance required to reject the null hypothesis, p=0.05/3 = 0.0167. We found that conditions did not differ significantly over small case libraries, but that with large case libraries MAC/FAC over generalizations alone significantly outperformed both other MAC/FAC techniques. We adjusted the significance standard for number of consistency checks performed in the same manner.

For comparison of number of consistency checks by case library size we performed pairwise t- tests; even using Bonferroni’s correction for repeated assessment, we found statistically significant differences across conditions and case library size.

Why performance of MAC/FAC over cases improves then worsens: performance of the MAC/FAC over cases alone condition improves to nearly 100% accuracy with case library of size 4 before dropping to 75% with case libraries of size 7. This makes perfect sense if you consider how consistency checks and reretrieval works in our experiment. Recall that, if MAC/FAC does not determine an answer that passes the consistency check, it performs one additional retrieval without the cases it has already checked. Furthermore, MAC/FAC retrieves a maximum of three cases, and often fewer (the top three mappings MAC/FAC returns are not necessarily from different cases).

Since there are only four confounds for each case in this study, with a case library of size four, the training set is extremely likely to contain a match to the test case. In this experiment a case library of size four is a sweet spot where the case library is both likely to contain a match and have MAC/FAC over cases retrieve it, even if it is only because after performing reretrieval MAC/FAC over a case library of this size has likely considered every possible case as a match.. Accuracy

goes down with larger case library sizes because there are potentially more confounds in each case library, so MAC/FAC might not exhaust higher-scored by less accurate matches before retrieving a lower-ranked but accurate match.

We expect that, with larger case libraries, we would see a steady, linear increase in accuracy of MAC/FAC over cases. The other conditions do not display the same behavior because the structure of generalizations leads MAC/FAC to find a more accurate match sooner, regardless of case library size.