After performing the syntactic substitutions (See section 
, page ) and the
translations required to make time dependence explicit
(See section , page ), the semantics of the model fragment form may be
defined after making some preliminary definitions:
A literal is time dependent if its relation constant names a time dependent relation or it contains a time dependent term. A term is time dependent if it has a function constant that names a time dependent function or a quantity function, or if it contains a time dependent term.
A literal is time independent if it is not time dependent.
The conditions and consequences may be separated into their time-dependent and time-independent portions.
Let temporal conditions be the time dependent conditions in conditions, and atemporal conditions be the time independent ones. Let temporal consequences be the time dependent consequences in consequences, and atemporal consequences be the time independent ones.
We can divide the axioms into four portions:
If an object is an instance of name, the following definitional axiom defines invariant properties of the object:
where attribute axiom is
when type is
provided, quantity axiom is the axiom implied by the
quantity function definition for quantity, and the
participant axiom is 
when participant
type is provided.
The following axiom defines when an instance of name is active:
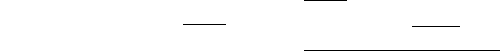
That is, m is an active instance of name exactly when m is an instance of name (this ensures that its participants are defined and its atemporal conditions are satisfied), it is an active instance of each of its superclasses, and its temporal conditions are satisfied.
We provide an axiom that specifies that the temporal
consequences hold whenever an instance is active:
If there are participants or conditions, then these define both
necessary and sufficient conditions for an object to be an instance of
name. The form of the axiom depends on whether or not
name has any superclasses. If there are explicit
superclasses, then any object that is an instance of the superclasses
and also satisfies the additional restrictions is an instance of
name. If name does not have any explicit
superclasses, then the existence of participants that satisfy the
conditions is sufficient to imply the existence of an instance.
If there are neither participants nor conditions, then there is no axiom defined to infer that an object is an instance of name. It is, of course, possible for this to be inferred by user specified axioms via defRelation or other model fragment definitions. When there are no participants or conditions, the defModelFragment form is equivalent to the defEntity form.
If name has explicit superclasses (i.e. the :subclass-of clause is not empty), the following axiom is used:
If there are no explicit superclasses, but there are either participants or conditions, then the following axiom is used:
