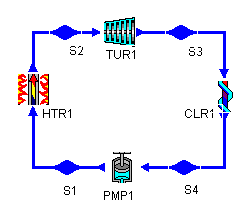
Figure 1: a Rankine cycle


The operating limits are
The regeneration cycle we examine will operate under the same limits. For reference, the Rankine cycle layout is shown below.

Figure 1: a Rankine cycle
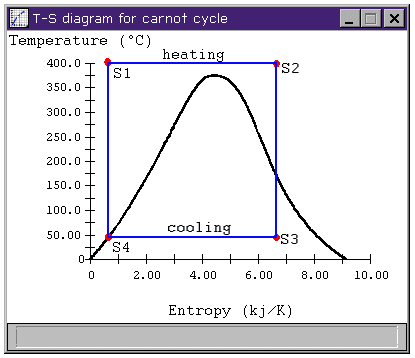
Figure 2: Carnot cycle T-s diagram
and the average temperature of heat rejection is
For more efficient cycles, we would like to add heat at a higher temperature and reject it at a lower temperature.
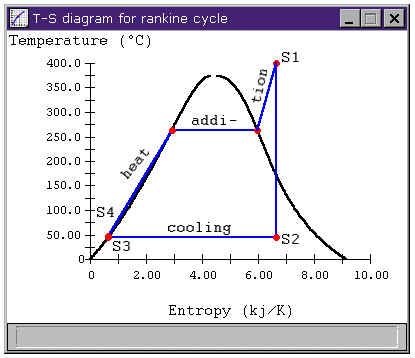
Figure 3: Rankine cycle T-s diagram
Which is the same answer we get applying the usual h = Wnet / Qhi relation.
The idea behind regeneration is that we split the turbine into high-pressure and low-pressure stages and do the same for the pump. Then, we can divert some of the heat in the fluid as it leaves the high-pressure turbine and add it to the cool fluid leaving the low-pressure pump, thereby sending fluid with a higher temperature to the heater. We'll look at this in more detail in a minute, but now we know enough to construct the Rankine cycle with regeneration.
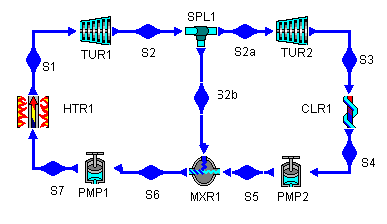
Figure 4: a Rankine cycle with regeneration
What pressure do we choose for the extracted feedwater? We don't know yet, so we'll choose 200 kPa, which gives the two turbines pressure ratios of 25 and 20. This makes them roughly equal and keeps either one from having an astronomically high pressure ratio. (The original Rankine cycle had a turbine PR equal to 500!) Later, when we have the cycle solved and we can let CyclePad do sensitivity analyses, we will see if another pressure works better.
The splitter is used to draw some of the working fluid from the high-pressure turbine stage and direct it towards the mixer. The assumption we make here is that the splitter is isoparametric. This means that the stuff exiting the splitter is the same as the stuff entering it.
We might think that this would be advantageous to regeneration so that we could send only saturated vapor (which has higher enthalpy) to the low-pressure turbine and get more work out of it and send the low quality remainder down to heat the water entering the high-pressure pump. So why not do this? Let's try it. We can retract the isoparametric assumption and instead assume the stuff entering the low-pressure turbine is a saturated vapor. Then when our other assumptions for this cycle have been made, we will see that the efficiency has changed by a few hundredths of a percent and we see that such an approach does not improve cycle efficiency by much. Our high-pressure pump condition (S6 below) requires that the total enthalpy H (not h) entering the high-pressure pump is constant, so the lower quality of the steam entering the mixer requires a higher mass flow into the mixer, nearly negating the benefit of the higher h steam that enters the low-pressure turbine. That is, we could send lower h stuff to the pump, but we'd have to send more of it. Of course, any efficiency improvement is better than none, but it isn't always realistic to assume that we can use the special splitter than separates vapor from liquid, so we'll continue using the isoparametric splitter.
What pressure should the water at this state have? This water, which enters the pump at the cooler pressure, needs to be pumped up to the pressure of the water extracted from the high-pressure turbine. This is a matter of simple hydrostatics: if we make it lower, the higher pressure extract water will flow backward through the low-pressure pump and, if we make it higher, the low pressure pump water will flow backward through the splitter.
We could just set this pressure at 200 kPa, the pressure we set at the high-pressure turbine outlet. However, the better approach is to tell CyclePad to make the two pressures equal, using the "Equate T(S5) to another parameter" option. This way, when we need to experiment with different feedwater pressures, we don't need to make the change in two places. Another equivalent solution is to declare MXR1 to be isobaric.
Our whole purpose in adding heat to this water is to raise its temperature before it enters the heater and improve the cycle efficiency. The water exiting the low-pressure pump is only at 46 C and the water entering the heater in the original Rankine cycle was at about the same temperature (adding pressure to an incompressible fluid doesn't raise its temperature much). How high can we heat the water to improve this?
The only limit we really need to consider is the practical use of the pump. We make sure the water entering the pump in a simple Rankine cycle is a saturated fluid because pumps cannot handle vapor very well. We have the same consideration here. We want to heat this water up as much as we can, but not so much that some of it starts to vaporize again. We recall that this is the state of a saturated liquid. This is our assumption for the high-pressure pump inlet: it is saturated with quality = 0.
We now have made the changes needed to add a regeneration stage to our Rankine cycle. Here are the new efficiencies and the ones of the plain Rankine cycle for comparison. Also shown is the percent gain in power output of the modified cycle when supplied with the same heat as the unmodified Rankine cycle and the mean temperatures of heat addition for both cycles.
| Cycle Efficiencies | Unmodified Rankine Cycle |
Rankine Cycle with Regeneration |
|---|---|---|
| Carnot efficiency | 52.6% | 52.6% |
| Thermal efficiency | 36.2% | 38.4% |
| % Increase in Power Generation | 0% | 6.1% |
| mean temperature of heat addition | 226.7 C | 251.5 C |
Can we do even better? We made only one decision that was somewhat arbitrary in picking numbers, choosing the outlet pressure of the high-pressure turbine so that the two turbines would have similar (and low) pressure ratios. However, while that is a worthwhile choice considering the economics of turbine purchasing, it may not yield the optimal cycle efficiency.
We can examine the relationship between the thermal efficiency of our regenerative cycle and the feedwater pressure (the pressure at S2). The sensitivity analysis looks like this
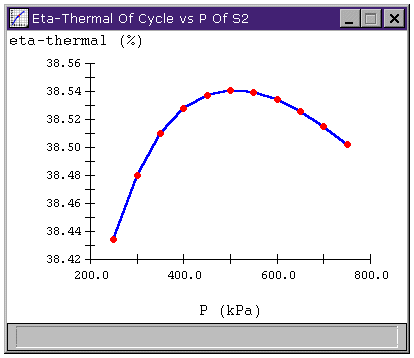
Figure 5: Effect of varying feedwater pressure on
cycle efficiency of Rankine cycle with regeneration.
Of course, the limit on the improvement made by the regeneration stage seems to be that we can only add so much heat to the fluid entering the high-pressure pump before the fluid begins to evaporate, damaging the pump. At higher pressures, the working fluid can contain more heat before it begins to boil away. So, we could repeat the process several times: add some heat until boiling almost occurs, then pump to a higher pressure, then add more heat, and so on.
For instance, by adding another regeneration stage to the design above, and hunting a little to find good feedwater pressures, we can improve the cycle's thermal efficiency to about 39.5%, which is a significant improvement from the 38.4% with one regeneration stage. A third regeneration stage brings the efficiency to just over 40%. How far can this go? For a Rankine cycle where the steam enters the boiler as a superheated gas, we can never achieve the efficiency of the Carnot cycle, even with an infinite number of regeneration stages. (If the steam entered the turbine as a saturated vapor, we could, in theory, achieve Carnot efficiency with infinite regeneration stages, but such cycles are impractical for other reasons besides the need for infinite stages.)
The real limit is economic, since having the extra extraction stages and pumps adds to the cost of the plant. At some point, the cost of the extra equipment outweighs the savings due to increased cycle efficiency. Practical plants seldom have more than five regeneration stages.
Whalley, P.B. 1992. Basic Engineering Thermodynamics. Oxford University Press. ISBN: 0-19-856255-1
Haywood, R.W. 1980. Analysis of Engineering Cycles. Pergamon Press. ISBN: 0-08-025440-3
Contributed by: M. E. Brokowski
Initial Entry: 12/10/97
Last Edited: 12/15/97
For comments or suggestions please contact CyclePad-librarian@cs.northwestern.edu