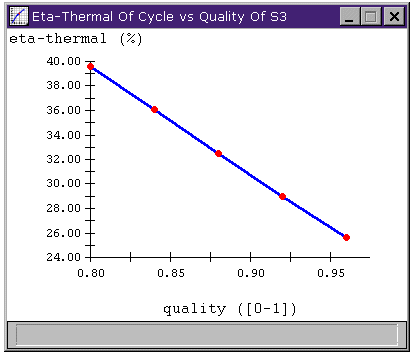
Figure 1: The relation between increased turbine
outlet quality and decreased cycle


We will occasionally encounter reheated cycles whose efficiency is not as high as that of the original Rankine cycle operated between the same high and low pressure limits. (For the case presented in our reheat example they are both nearly identical at 40%.) However, we can see that adding reheat actually improves thermal efficiency compared to a Rankine cycle operated at the same outlet dryness. This comparison is typically more appropriate for practical cycles, where turbine damage is a consideration and we cannot allow the steam to exit at such a low pressure. Another glance at the graph of turbine outlet quality and cycle efficiency (reproduced below) shows that operating the Rankine cycle used in our previous example at 90% outlet quality would have lead to a cycle efficiency down around 30%, compared to the 40% we got by adding the reheat stage.

Figure 1: The relation between increased turbine
outlet quality and decreased cycle
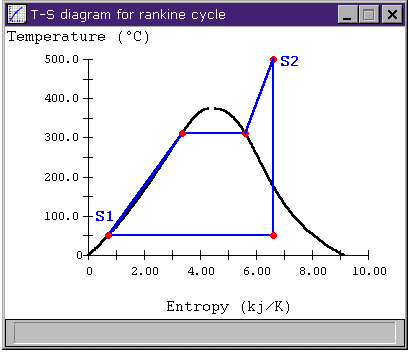
2-A: Rankine Cycle
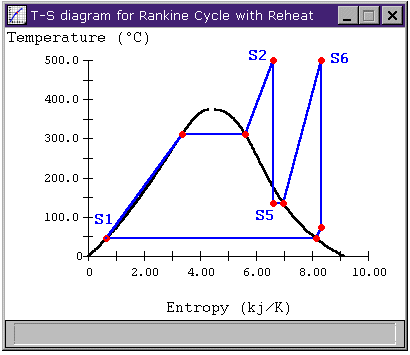
2-B: Rankine Cycle with Reheat
Recall that a Carnot cycle has all of its heat addition at the same temperature, which is the highest temperature in the cycle. When we look to improve a cycle's efficiency, we often consider the mean temperature of heat addition and the mean temperature of heat rejection. These are simply what the temperature would have been if the same amount of heat had been added (or rejected) all at one temperature, allowing us to treat the cycle as a Carnot cycle operating between these two temperatures. For reversable heat transfer, the average temperature of heat addition is Qin / DS and the average temperature of heat rejection is Qout / DS. For more efficient cycles, we would like to add heat at a higher temperature and reject it at a lower temperature.
Knowing this, let's look at Figure 2 again. In the Rankine cycle, the above equation tells us we are adding heat between states S1 and S2 at an average temperature of about 260 C. The reheat cycle has heat addition from S1 to S2 and again from S5 to S6, also at an average temperature of about 260 C, which doesn't surprise us given the nearly equal efficiencies of the two cycles.
Just looking at the T-s diagram (Figure 2-B) for the reheat cycle, it appears that we might be able to raise this mean temperature by allowing the fluid to leave the turbine at S5 at a higher pressure. Figure 3 shows a sensitivity analysis that confirms the benefit of a higher reheat pressure for improving cycle efficiency.
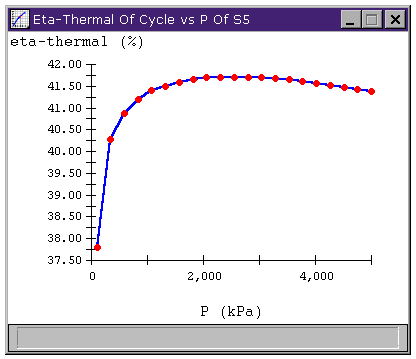
Figure 3: Rankine Cycle with reheat
Improving Cycle Efficiency with Higher Reheat Pressure
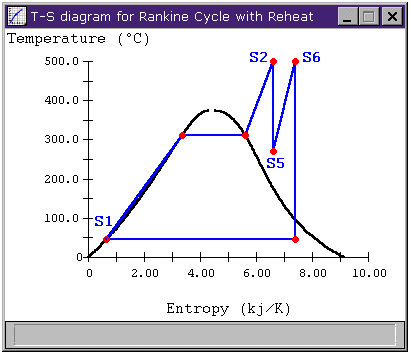
Figure 4: Rankine Cycle with Reheat
and Higher Mean Temperature of Heat Addition
Download the CyclePad design of the original Rankine Cycle with Reheat or the modified Rankine Cycle with Reheat.
Whalley, P.B. 1992. Basic Engineering Thermodynamics. Oxford University Press. ISBN: 0-19-856255-1
Contributed by: Peter B. Whalley, Kenneth D.
Forbus, M. E. Brokowski
Initial Entry: 9/5/97
Last Edited: 12/9/97
For comments or suggestions please contact cyclepad-librarian@cs.northwestern.edu